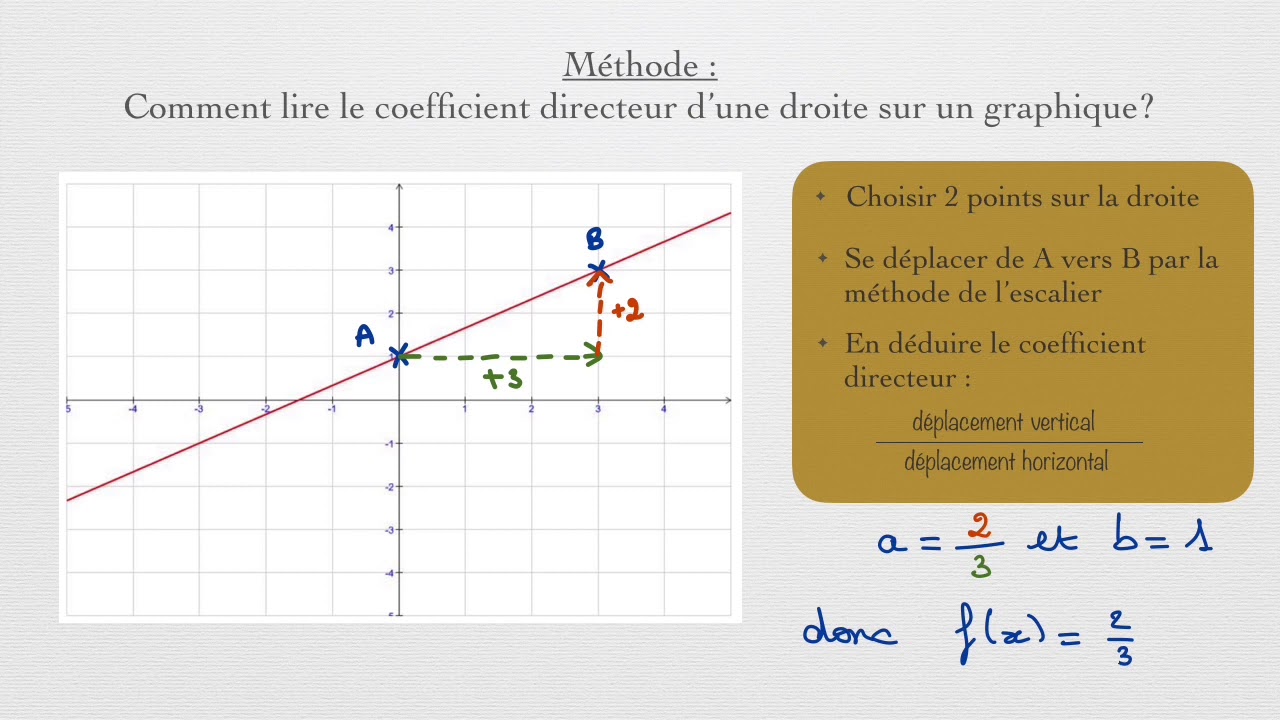
En mathématiques, la notion de pente est omniprésente. Mais que se cache-t-il derrière cette idée de pente, et comment la quantifier ? C'est là qu'intervient le coefficient directeur. Cet article vous propose de décrypter ce concept essentiel, de son origine à ses applications pratiques, en passant par les difficultés qu'il peut parfois présenter.
Le coefficient directeur, aussi appelé pente ou coefficient angulaire, représente la variation verticale d'une droite pour une variation horizontale unitaire. Il permet de quantifier l'inclinaison d'une droite dans un plan cartésien. Une pente forte se traduit par un coefficient directeur élevé, tandis qu'une pente faible correspond à un coefficient directeur proche de zéro. Une droite horizontale a un coefficient directeur nul.
L'histoire du coefficient directeur est intimement liée au développement de la géométrie analytique, initiée par Descartes et Fermat au XVIIe siècle. L'idée de relier l'algèbre et la géométrie a permis de représenter des droites par des équations, et ainsi de définir précisément la notion de pente. Cette avancée majeure a ouvert la voie à de nombreux développements en mathématiques et en physique.
Comprendre la signification du coefficient directeur est crucial pour interpréter correctement les relations entre des variables. En économie, par exemple, il peut représenter l'élasticité-prix de la demande. En physique, il peut traduire la vitesse d'un objet en mouvement uniforme. Sa maîtrise est donc indispensable pour analyser et modéliser de nombreux phénomènes.
Un des principaux problèmes liés à la compréhension du coefficient directeur réside dans son interprétation. Il est important de bien saisir que ce n'est pas la mesure de l'angle que forme la droite avec l'axe horizontal, mais bien le rapport entre la variation verticale et la variation horizontale.
Le coefficient directeur d'une droite se calcule à partir des coordonnées de deux points distincts de cette droite. Si on a les points (x1, y1) et (x2, y2), le coefficient directeur (m) est donné par la formule : m = (y2 - y1) / (x2 - x1).
Exemple : Si une droite passe par les points (1, 2) et (4, 8), son coefficient directeur est (8 - 2) / (4 - 1) = 6 / 3 = 2. Cela signifie que pour chaque unité de déplacement horizontal, la droite monte de deux unités verticalement.
Avantages du coefficient directeur:
1. Quantifier l'inclinaison : Permet de comparer l'inclinaison de différentes droites.
2. Modéliser des phénomènes : Utile pour représenter mathématiquement des relations linéaires.
3. Prédire des valeurs : Permet d'extrapoler ou d'interpoler des valeurs sur une droite.
FAQ:
1. Qu'est-ce que le coefficient directeur d'une droite verticale ? Une droite verticale a un coefficient directeur indéfini.
2. Comment interpréter un coefficient directeur négatif ? Il indique une droite décroissante.
3. Quelle est la relation entre le coefficient directeur et l'équation d'une droite ? L'équation d'une droite est de la forme y = mx + b, où m est le coefficient directeur et b l'ordonnée à l'origine.
4. Comment trouver la pente d'une courbe ? La pente d'une courbe en un point donné est donnée par la dérivée de la fonction en ce point.
5. Que signifie un coefficient directeur égal à zéro ? Cela correspond à une droite horizontale.
6. Comment calculer le coefficient directeur à partir d'une équation ? Si l'équation est sous la forme y = mx + b, le coefficient directeur est m.
7. Comment représenter graphiquement une droite connaissant son coefficient directeur ? On peut utiliser le coefficient directeur et l'ordonnée à l'origine pour tracer la droite.
8. Qu'est-ce que la signification géométrique du coefficient directeur ? Il représente le rapport entre le déplacement vertical et le déplacement horizontal d'une droite.
Conseils et astuces : Pour bien maîtriser le coefficient directeur, il est important de s’exercer à le calculer à partir de différents points et d’interpréter sa valeur dans des contextes variés.
En conclusion, le coefficient directeur est une notion fondamentale en mathématiques. Il permet de quantifier l'inclinaison d'une droite et de modéliser des relations linéaires dans divers domaines. Sa compréhension est essentielle pour interpréter correctement les données et prédire des valeurs. En maîtrisant ce concept, vous disposerez d'un outil puissant pour analyser et comprendre le monde qui nous entoure. N'hésitez pas à explorer davantage les ressources en ligne et les manuels pour approfondir vos connaissances sur ce sujet essentiel.
Le saint graal du fusil a pompe decryptage du god roll dans destiny 2
Eveillez leurs talents musicaux le monde des instruments pour enfants
Revolution de lintelligence artificielle innovations recentes











.png)