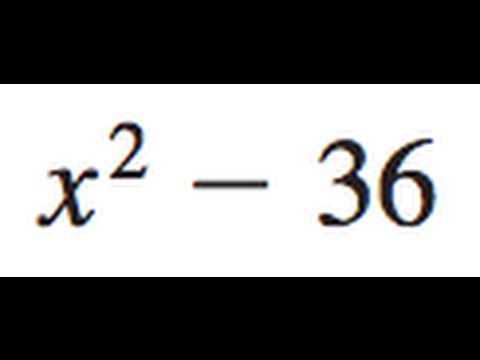Vous êtes bloqué face à l'expression x² - 49 ? Pas de panique ! Factoriser cette expression est plus simple qu'il n'y paraît. Ce guide pratique vous dévoile les secrets de la factorisation de x² - 49, des bases aux techniques plus avancées.
La factorisation, c'est un peu comme décomposer un puzzle en ses pièces élémentaires. Dans le cas de x² - 49, le but est de transformer cette expression en un produit de facteurs plus simples. Comprendre ce processus est essentiel en algèbre et vous ouvrira les portes de concepts mathématiques plus complexes.
L'expression x² - 49 est un cas particulier d'une identité remarquable : la différence de deux carrés. Cette identité est un outil fondamental en mathématiques, utilisée depuis des siècles pour simplifier les expressions algébriques. Sa maîtrise est un atout majeur pour résoudre des équations, simplifier des fractions et bien plus encore.
L'un des principaux problèmes que les étudiants rencontrent avec la factorisation de x² - 49 est de reconnaître cette fameuse différence de deux carrés. Souvent, ils se perdent dans des calculs complexes alors que la solution est à portée de main. Ce guide vous aidera à identifier rapidement ce type d'expression et à appliquer la méthode de factorisation appropriée.
La factorisation de x² - 49 repose sur l'identité remarquable a² - b² = (a + b)(a - b). Dans notre cas, x² joue le rôle de a² et 49 joue le rôle de b². Comme 49 est le carré de 7 (7² = 49), on peut réécrire l'expression sous la forme x² - 7². En appliquant l'identité remarquable, on obtient la factorisation suivante : x² - 49 = (x + 7)(x - 7).
Voici les étapes pour factoriser x² - 49 :
1. Identifier la différence de deux carrés : reconnaissez que x² est le carré de x et 49 est le carré de 7.
2. Appliquer l'identité remarquable : utilisez la formule a² - b² = (a + b)(a - b) avec a = x et b = 7.
3. Écrire la factorisation : x² - 49 = (x + 7)(x - 7).
Exemples concrets :
1. Résoudre l'équation x² - 49 = 0. Grâce à la factorisation, on obtient (x+7)(x-7) = 0, donc x = 7 ou x = -7.
2. Simplifier la fraction (x² - 49) / (x - 7). Après factorisation, on obtient (x+7)(x-7) / (x-7) = x+7 (pour x différent de 7).
FAQ :
1. Qu'est-ce que la factorisation ? Décomposer une expression en un produit de facteurs.
2. Pourquoi factoriser x² - 49 ? Pour simplifier des expressions ou résoudre des équations.
3. Quelle est l'identité remarquable utilisée ? a² - b² = (a + b)(a - b).
4. Que représentent a et b dans notre cas ? a = x et b = 7.
5. Quel est le résultat de la factorisation de x² - 49 ? (x + 7)(x - 7).
6. Comment vérifier la factorisation ? En développant le produit (x+7)(x-7).
7. Quand utiliser la factorisation de x² - 49 ? Pour simplifier des expressions, résoudre des équations, étudier des fonctions.
8. Existe-t-il d'autres identités remarquables ? Oui, comme (a+b)² et (a-b)².
Conseils et astuces : Mémorisez l'identité remarquable a² - b² = (a + b)(a - b). Pratiquez la factorisation sur d'autres exemples similaires.
En conclusion, factoriser x² - 49 est une compétence essentielle en algèbre. Maîtriser cette technique vous permettra de simplifier des expressions complexes, de résoudre des équations et de progresser vers des concepts mathématiques plus avancés. La clé réside dans la reconnaissance de la différence de deux carrés et l'application de l'identité remarquable correspondante. N'hésitez pas à pratiquer régulièrement pour intégrer pleinement cette méthode et l'utiliser avec aisance. La factorisation ouvre la voie à une compréhension plus profonde des mathématiques et à la résolution de problèmes plus complexes, alors lancez-vous et explorez les possibilités qu'elle offre !
Rouler sans se ruiner le guide des rollers pas chers
Baume levres burts bees coco poire decouverte et avantages
Mucus dans les selles de lenfant comprendre et reagir