Hoe vaak kom je in het dagelijks leven wiskundige vergelijkingen tegen? Misschien meer dan je denkt. Van het berekenen van kortingen in de supermarkt tot het bepalen van de benodigde hoeveelheid verf voor je muur, wiskunde speelt een subtiele maar cruciale rol. Vandaag duiken we in een specifiek type vergelijking: de lineaire vergelijking, aan de hand van het voorbeeld "als y = 3x - 1, vind dan y voor x = 5".
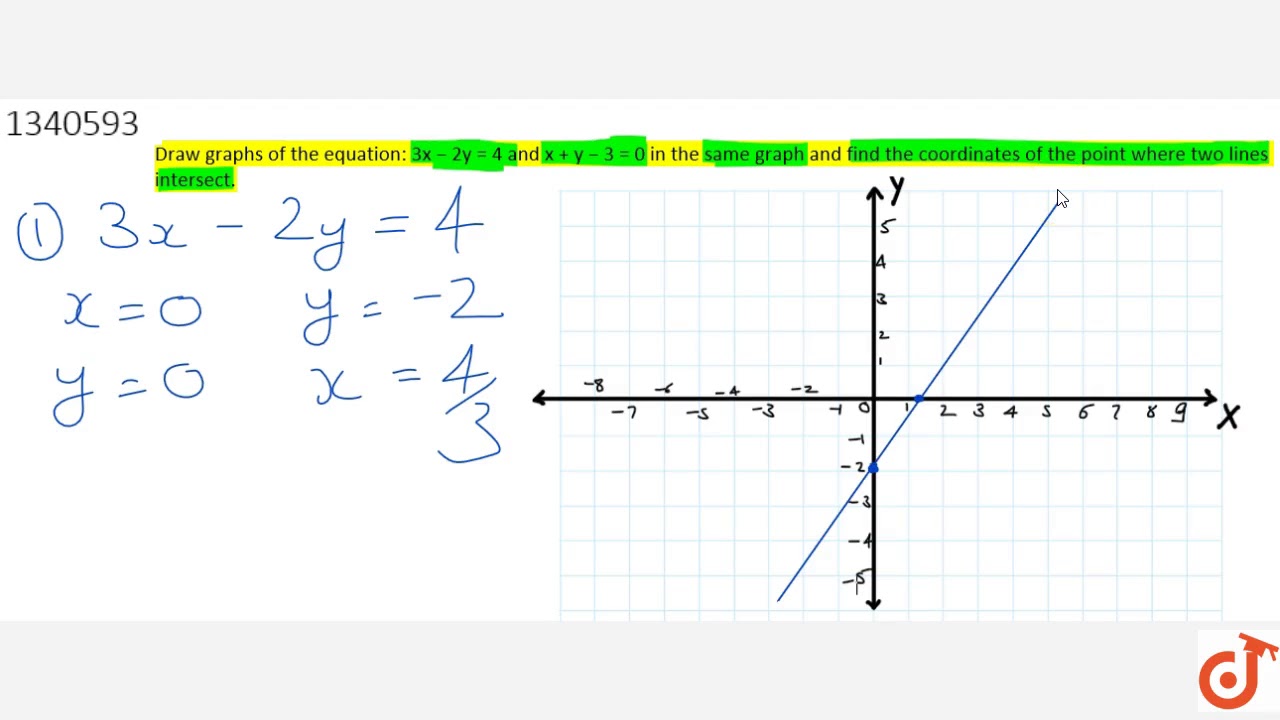
Lineaire vergelijkingen, zoals y = 3x - 1, beschrijven een rechte lijn op een grafiek. Ze verbinden twee variabelen, in dit geval x en y, in een rechtlijnige relatie. Het begrijpen van deze relatie is fundamenteel voor vele gebieden, van natuurkunde en economie tot computerprogrammering en data-analyse.
De vergelijking "als y = 3x - 1, vind dan y voor x = 5" vraagt ons om de waarde van y te berekenen wanneer x gelijk is aan 5. Dit is een klassiek voorbeeld van het oplossen van een lineaire vergelijking en vormt de basis voor complexere wiskundige concepten.
De oorsprong van lineaire vergelijkingen gaat ver terug in de geschiedenis. Wiskundigen uit verschillende culturen hebben bijgedragen aan de ontwikkeling van de theorie achter deze vergelijkingen. Van de oude Grieken tot de Arabische wiskundigen, de zoektocht naar het begrijpen van lineaire relaties heeft de wiskunde eeuwenlang gevormd.
Het belang van lineaire vergelijkingen kan niet genoeg benadrukt worden. Ze vormen de basis voor het modelleren van talloze real-world scenario's. Denk aan het voorspellen van verkooptrends, het berekenen van de snelheid van een bewegend object of het analyseren van financiële gegevens. Het beheersen van lineaire vergelijkingen opent de deur naar een dieper begrip van de wereld om ons heen.
Om "als y = 3x - 1, vind y voor x = 5" op te lossen, vervangen we x door 5 in de vergelijking: y = 3 * 5 - 1. Dit vereenvoudigt tot y = 15 - 1, wat resulteert in y = 14.
Veelgestelde vragen:
1. Wat is een lineaire vergelijking? Een lineaire vergelijking beschrijft een rechte lijn en verbindt twee variabelen in een rechte relatie.
2. Hoe los je "als y = 3x - 1, vind y voor x = 5" op? Vervang x door 5 in de vergelijking en bereken y.
3. Wat is het belang van lineaire vergelijkingen? Ze vormen de basis voor veel wiskundige modellen en real-world toepassingen.
4. Waar kan ik meer leren over lineaire vergelijkingen? Online bronnen zoals Khan Academy en wiskundeboeken bieden uitgebreide informatie.
5. Wat is de helling in y = 3x - 1? De helling is 3, wat aangeeft hoe steil de lijn is.
6. Wat is het snijpunt met de y-as in y = 3x - 1? Het snijpunt is -1, het punt waar de lijn de y-as snijdt.
7. Kan "als y = 3x - 1" gebruikt worden voor voorspellingen? Ja, je kunt toekomstige waarden van y voorspellen op basis van gegeven x-waarden.
8. Zijn er online tools om lineaire vergelijkingen op te lossen? Ja, er zijn diverse online calculators en grafische tools beschikbaar.
Tips en trucs: Oefening baart kunst! Probeer verschillende waarden voor x in de vergelijking te substitueren om je begrip te versterken.
Lineaire vergelijkingen, zoals geïllustreerd door "als y = 3x - 1, vind dan y voor x = 5", vormen een essentieel onderdeel van de wiskunde en hebben talloze toepassingen in de realiteit. Van het begrijpen van simpele relaties tot het modelleren van complexe systemen, de kracht van lineaire vergelijkingen is onmiskenbaar. Door de basisprincipes te beheersen, open je de deur naar een dieper begrip van de wereld om ons heen en leg je de basis voor verdere wiskundige exploratie. Begin vandaag nog met het oefenen en ontdek de fascinerende wereld van lineaire vergelijkingen! Verdiep je in de theorie, experimenteer met verschillende voorbeelden en ontdek hoe deze krachtige tool je kan helpen bij het oplossen van problemen en het ontrafelen van patronen in data. De mogelijkheden zijn eindeloos, dus ga aan de slag en ontdek de magie van lineaire vergelijkingen!
De mooiste psalm 23 vertalingen ontdekken
Jeff lock and key rainsville al uw sleutel tot veiligheid
De kinderen van adam en eva de oorsprong van de mensheid
