Ever wondered about the hidden energy within a stretched rubber band or a perched bird? That's potential energy, waiting to be unleashed. Understanding how to calculate potential energy is key to grasping fundamental principles in physics, from roller coasters to the orbits of planets. This guide will delve into the intricacies of potential energy calculations, providing you with the tools to unlock this fascinating concept.
Potential energy, in its simplest form, represents the energy stored within an object due to its position or configuration. Imagine a ball held high above the ground. It possesses gravitational potential energy because gravity can pull it downwards, converting that stored energy into kinetic energy (motion). Similarly, a compressed spring stores elastic potential energy, ready to spring back to its original shape. Calculating potential energy allows us to quantify this stored energy and predict the object's behavior when it's released.
The concept of potential energy traces its roots back to the 19th century with the development of classical mechanics. Early physicists like James Prescott Joule and William Thomson (Lord Kelvin) played crucial roles in establishing the principles of energy conservation and the relationship between potential and kinetic energy. The ability to calculate potential energy became essential for advancements in engineering, astronomy, and other fields. A key issue in applying these calculations lies in accurately defining the system and its boundaries. Choosing the appropriate reference point for gravitational potential energy, for example, is crucial for obtaining correct results.
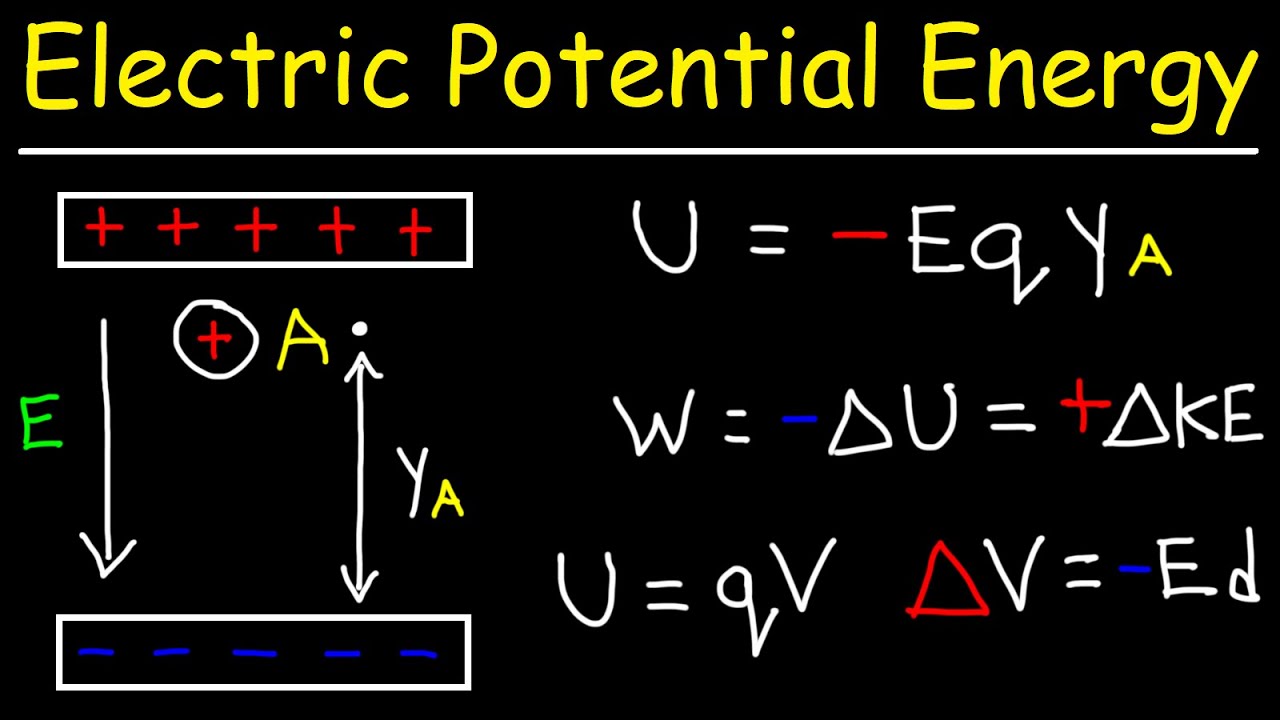
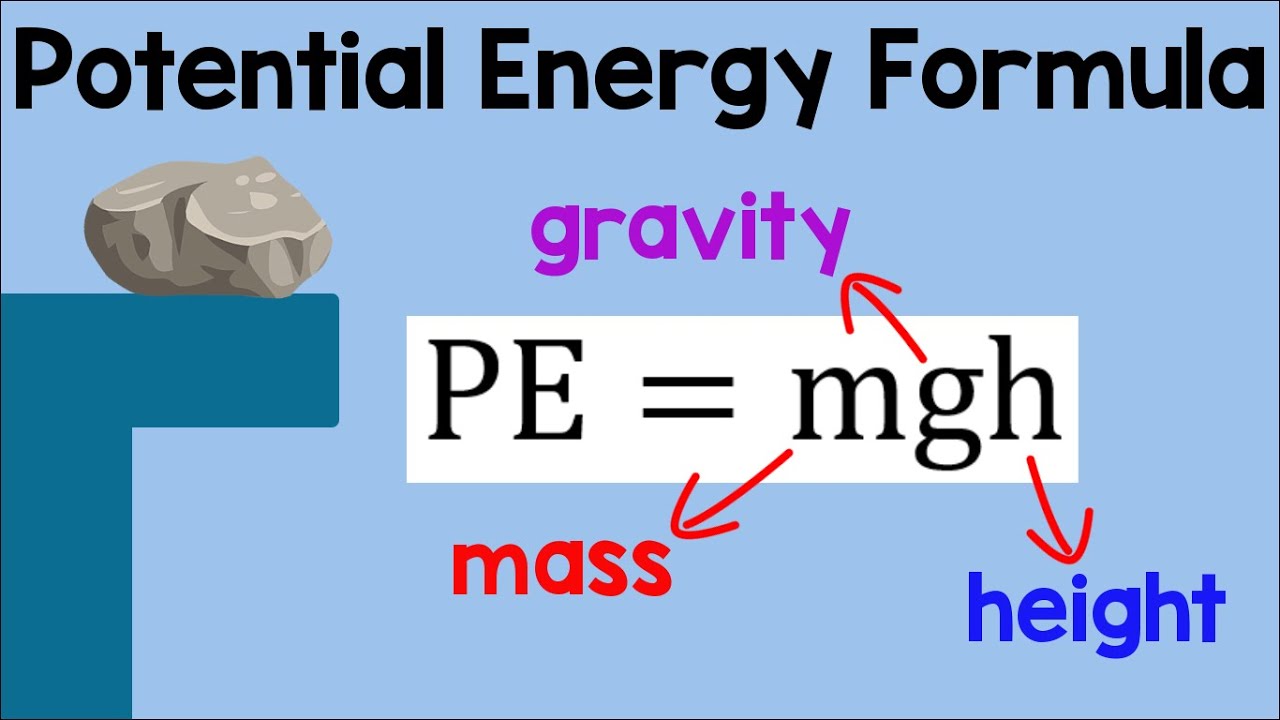
There are two primary types of potential energy: gravitational and elastic. Gravitational potential energy depends on an object's mass, the acceleration due to gravity (approximately 9.8 m/s² on Earth), and its height above a reference point. The formula for gravitational potential energy is PE = mgh, where PE represents potential energy, m is mass, g is gravity, and h is height. Elastic potential energy, on the other hand, is the energy stored in a stretched or compressed spring. It is calculated using PE = (1/2)kx², where k is the spring constant (a measure of the spring's stiffness) and x is the displacement from the spring's equilibrium position. For example, a 1 kg ball held 2 meters above the ground has a gravitational potential energy of (1 kg)(9.8 m/s²)(2 m) = 19.6 Joules.
Calculating potential energy isn't just a theoretical exercise; it has real-world applications. Engineers use it to design safe roller coasters, ensuring that the cars have enough potential energy at the top of a hill to complete the ride. Architects consider potential energy when designing structures, taking into account the stability of beams and columns. Physicists use potential energy calculations to study planetary motion and celestial mechanics.
Benefit 1: Predicting Motion. Knowing an object's potential energy allows us to predict its future motion and speed when that energy converts to kinetic energy. Example: A roller coaster's speed at the bottom of a hill can be predicted based on its potential energy at the top.
Benefit 2: Designing Efficient Systems. Calculating potential energy is crucial for designing efficient energy storage systems, such as pumped hydro power plants, which store energy by pumping water uphill. Example: Engineers optimize the height difference in pumped hydro to maximize energy storage.
Benefit 3: Understanding Stability: Potential energy helps determine the stability of structures. A lower potential energy signifies greater stability. Example: A broader base lowers the center of gravity and thus the potential energy of a structure, making it more stable.
Action Plan: 1. Identify the type of potential energy (gravitational or elastic). 2. Gather necessary values (mass, height, gravity, spring constant, displacement). 3. Apply the appropriate formula. Successful example: Correctly calculating the energy needed to launch a satellite into orbit.
Checklist: ☐ Identify type of potential energy. ☐ Determine necessary variables. ☐ Apply correct formula. ☐ Check units.
Step-by-step guide: 1) Determine whether the system involves gravitational or elastic potential energy. 2) Identify the known and unknown variables. 3) Select the appropriate formula (PE=mgh or PE=(1/2)kx²). 4) Substitute the known values into the formula. 5) Calculate the potential energy. 6) Verify the units (Joules).
Recommended resources: Khan Academy (website), University Physics (book), Physics Toolbox Sensor Suite (app).
Advantages and Disadvantages of Potential Energy Calculations
| Advantages | Disadvantages |
|---|---|
| Predicts object behavior | Simplifications can lead to inaccuracies in complex systems |
| Enables efficient system design | Requires accurate measurements of parameters like height and spring constant |
| Helps analyze stability | Does not directly account for energy losses due to friction or other factors |
Best Practice 1: Clearly define the system and reference point. Best Practice 2: Use consistent units. Best Practice 3: Account for significant figures. Best Practice 4: Consider potential energy transformations. Best Practice 5: Double-check calculations.
Real Examples: 1. Roller coaster. 2. Stretched rubber band. 3. Water held in a dam. 4. Compressed spring in a toy. 5. Pendulum at its highest point.
Challenges and Solutions: 1. Complex systems - break down into simpler parts. 2. Non-ideal conditions - account for energy losses. 3. Variable forces - use calculus. 4. Choosing reference point - ensure consistency. 5. Experimental error - repeat measurements.
FAQ 1: What is potential energy? Answer: Stored energy due to position or configuration. FAQ 2: What are the types of potential energy? Answer: Gravitational and elastic. FAQ 3: What is the formula for gravitational potential energy? Answer: PE=mgh. FAQ 4: What is the formula for elastic potential energy? Answer: PE=(1/2)kx². FAQ 5: What are the units of potential energy? Answer: Joules. FAQ 6: How does potential energy relate to kinetic energy? Answer: They can convert into each other. FAQ 7: Why is understanding potential energy important? Answer: For understanding and predicting motion and stability. FAQ 8: What are some real-world applications of potential energy? Answer: Designing roller coasters, analyzing structural stability, and understanding planetary orbits.
Tips and tricks: Visualize the system, draw diagrams, practice with different scenarios, and break down complex problems into smaller, manageable parts.
In conclusion, understanding how to calculate potential energy is essential for anyone studying or working with physics. From predicting the trajectory of a projectile to designing efficient energy systems, the applications of this concept are vast. Mastering the formulas, considering the various types of potential energy, and being mindful of the best practices discussed will equip you to analyze and solve a wide range of physics problems. Potential energy calculations provide a window into the hidden energy within systems, allowing us to understand the world around us at a deeper level. Continue exploring this fascinating concept through further study and practical application to unlock its full potential.
When is the ballon dor ceremony your complete guide
Unlocking the secrets of amazon relay your guide to success
The turning point exploring snapping into love chapter 3





.png)