Ever wondered how a roller coaster keeps you glued to your seat as it loops the loop? Or how satellites manage to stay in orbit without plummeting back to Earth? The answers lie within the fascinating realm of circular motion, a fundamental concept in AP Physics. Understanding the equations that govern this type of motion unlocks a deeper understanding of the physical world around us, from the smallest atoms to the largest celestial bodies.
Circular motion, at its core, describes the movement of an object along a circular path. Unlike linear motion, where an object travels in a straight line, circular motion involves a constant change in direction, which means the object is always accelerating, even if its speed remains constant. This acceleration, known as centripetal acceleration, is always directed towards the center of the circle. This central seeking force responsible for this acceleration is called the centripetal force.
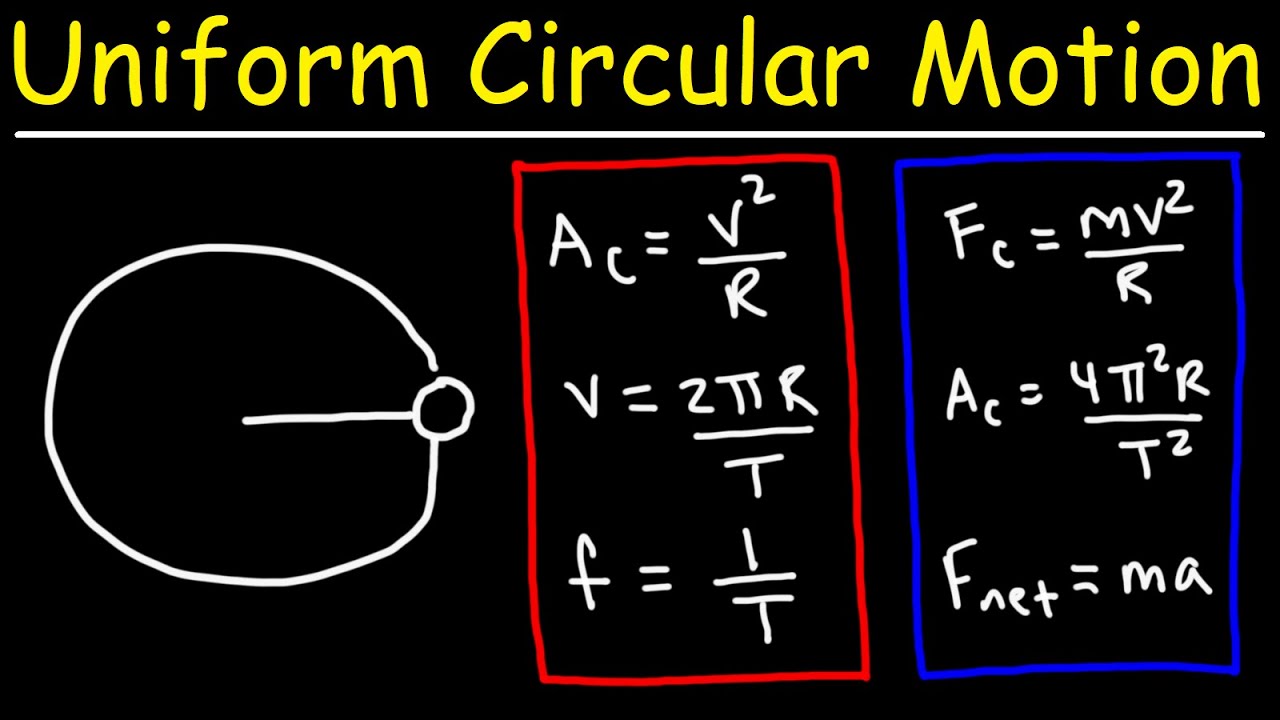
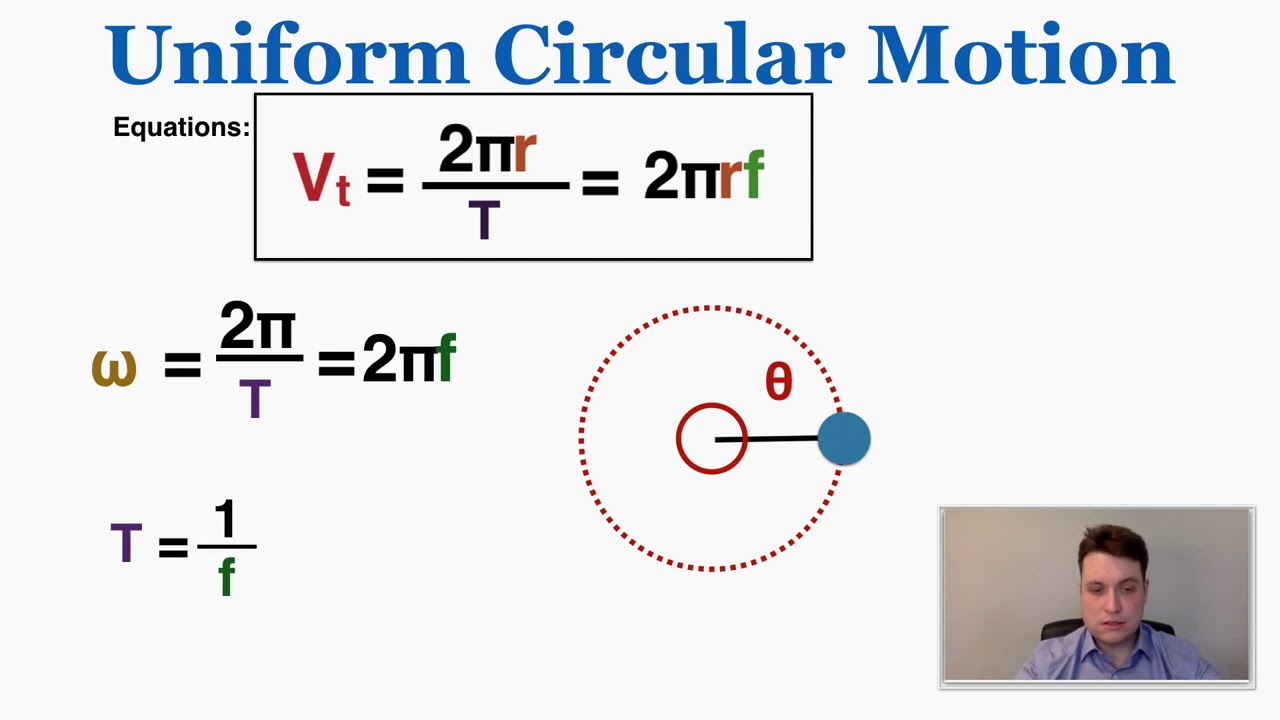
The equations for circular motion in AP Physics quantify these concepts. Centripetal force is given by Fc = mv2/r, where m is the mass of the object, v is its speed, and r is the radius of the circular path. Centripetal acceleration, closely related, can be calculated using ac = v2/r. These two formulas, seemingly simple, are powerful tools for understanding a wide range of phenomena.
The historical development of these equations is deeply intertwined with the evolution of classical mechanics. Scientists like Isaac Newton and Christiaan Huygens played key roles in formulating our understanding of circular motion. Newton's laws of motion, particularly his second law (F=ma), provide the foundation for understanding centripetal force. Huygens, on the other hand, contributed significantly to understanding the relationship between circular motion and oscillatory systems like pendulums.
The importance of understanding AP Physics circular motion equations extends far beyond the classroom. These principles are crucial in fields like engineering, astronomy, and even everyday life. Engineers use these concepts to design safe and efficient roller coasters, curves in roads, and rotating machinery. Astronomers rely on them to calculate the orbits of planets and satellites. Even something as simple as swinging a ball on a string demonstrates circular motion in action.
A simple example: Imagine a car turning a corner. The friction between the tires and the road provides the centripetal force necessary to keep the car moving in a circular path. If the car goes too fast, the frictional force may not be sufficient, causing the car to skid out of control.
One benefit of understanding these equations is the ability to predict the motion of objects in circular paths. For example, knowing the speed and radius of a carousel allows you to calculate the centripetal force required to keep a rider from flying off. Another benefit is understanding the relationship between different variables. For instance, you can see how increasing the speed of an object in circular motion requires a proportionally larger centripetal force.
One common challenge is distinguishing between centripetal force and centrifugal force. Centripetal force is the real force pulling an object towards the center, while centrifugal force is an apparent outward force felt by the object due to its inertia. It's important to remember that centrifugal force is not a real force in the inertial frame of reference.
A step-by-step guide to solving circular motion problems often involves identifying the forces acting on the object, determining the direction of the centripetal acceleration, and applying the relevant equations to solve for unknown quantities.
Advantages and Disadvantages of Working with Circular Motion Equations
| Advantages | Disadvantages |
|---|---|
| Predictive Power | Simplifications can sometimes be inaccurate in complex scenarios |
| Fundamental to understanding many physical phenomena | Requires a strong understanding of vector concepts |
FAQ: What is centripetal force? What is centripetal acceleration? What is the difference between uniform and non-uniform circular motion? How is circular motion related to simple harmonic motion? What are some real-world applications of circular motion? What is the role of friction in circular motion? What is the difference between tangential and radial acceleration? How does gravity affect circular motion?
Tips and Tricks: Draw free-body diagrams, pay attention to units, and remember that centripetal force is always directed towards the center of the circle.
In conclusion, understanding AP Physics circular motion equations is essential for grasping a fundamental concept that governs the universe around us. From the dizzying spins of amusement park rides to the precise orbits of satellites, these equations provide a powerful framework for understanding and predicting the motion of objects in circular paths. Mastering these concepts opens doors to a deeper appreciation of the physical world and paves the way for success in AP Physics and beyond. By delving into the history, applications, and problem-solving techniques associated with circular motion, students gain a valuable toolset for analyzing and interpreting a vast array of phenomena. The ability to analyze and solve circular motion problems is a critical skill for anyone pursuing a career in science or engineering, and the benefits of understanding these concepts extend far beyond the classroom.
Finding your perfect toyota rav4 prime a guide to purchasing
Revolutionizing tattoo stencils exploring affordable printer options
Boat lift canopies the ultimate guide to protecting your vessel